O Sistema de Avaliação da Educação Básica (SAEB)
É um conjunto de avaliações externas em larga escala que permite ao Inep realizar um diagnóstico da educação básica brasileira e de fatores que podem interferir no desempenho do estudante. Alguns problemas de Matemática. Se divirtam.
0
0
0
1
D1 – Identificar figuras semelhantes mediante o reconhecimento de relações de proporcionalidade. Observe as figuras desenhadas na malha quadriculada abaixo. A figura menor é uma redução da figura maior. Sobre as áreas dessas duas figuras podemos afirmar que:
a área da maior é o quádruplo da área da menor.
a área da maior é o quíntuplo da área da menor.
a área da maior é o dobro da área da menor.
a área da maior é o sêxtuplo da área da menor.
a área da maior é o triplo da área da menor.
2
D2 – Reconhecer aplicações das relações métricas do triângulo retângulo em um problema que envolva figuras planas ou espaciais. No processo de decolagem, um avião saiu do chão sob um determinado ângulo e se manteve em linha reta até atingir a cabeceira da pista, conforme o desenho ao lado. De acordo com esse desenho, quantos metros esse avião percorreu do momento em que saiu do chão até o momento em que atingiu a cabeceira da pista de decolagem?
9 600 metros.
1 600 metros.
40 000 metros.
280 metros.
200 metros.
3
D3 – Relacionar diferentes poliedros ou corpos redondos com suas planificações ou vistas. Qual é esse sólido?
Pirâmide de base triangular.
Prisma de base triangular.
Pirâmide de base hexagonal.
Prisma de base hexagonal.
Prisma de base quadrangular.
4
D4 – Identificar a relação entre o número de vértices, faces e/ou arestas de poliedros expressa em um problema. Pela Relação de Euler, tem-se que F + V = A + 2, onde F é o número de faces, V o número de vértices e, A o número de arestas. Qual é o número de faces de um poliedro convexo, que tem 9 arestas e 6 vértices?
7
6
4
3
5
5
D5 – Resolver problema que envolva razões trigonométricas no triângulo retângulo (seno, cosseno, tangente). Um telhado será instalado entre dois prédios de um condomínio, de forma que sua inclinação em relação ao prédio maior será de 53°, conforme representado no desenho a lado. Qual será o comprimento x desse telhado?
9,0
11,2
15,0
5,4
6,9
6
D6 – Identificar a localização de pontos no plano cartesiano. Observe o pentágono IJKLM representado no plano cartesiano abaixo. O ponto de coordenadas (– 2, – 1) é
M.
L.
J
I
K
7
D7 – Interpretar geometricamente os coeficientes da equação de uma reta. Observe abaixo a reta r de equação y = mx +n. De acordo com esse gráfico, os coeficientes m e n são
m > 0 e n < 0.
m > 0 e n > 0.
m < 0 e n < 0.
m > 0 e n = 0.
m < 0 e n > 0.
8
D8 – Identificar a equação de uma reta apresentada a partir de dois pontos dados ou de um ponto e sua inclinação. Um engenheiro urbanista tem o propósito de fazer um projeto de uma cidade, o qual duas avenidas paralelas devem ser construídas, a Av. S Um e a Av. T quatro. Depois de feitos os cálculos, obteve-se as equações das duas avenidas. A Av. S com equação 3x - 2y - 1 = 0 e a Av. T quatro com 9x - 6y + 2 = 0. Os coeficientes angulares das retas são respectivamente:
são diferentes e, valem 3/2 e 1/2.
ambos são iguais a 3/2.
ambos são iguais a 3 e 9.
ambos são iguais a –2 e –6.
ambos são iguais a 9 e 3.
9
D9 – Relacionar a determinação do ponto de interseção de duas ou mais retas com a resolução de um sistema de equações com duas incógnitas. O ponto de interseção das retas de equações x + 3y - 1 = 0 e x - y + 3 = 0 é:
(-2, -1).
(-1, -2).
(1, 2).
(1, -2).
(-2, 1).
10
D11 – Resolver problema envolvendo o cálculo de perímetro de figuras planas. Seu Artur deseja cercar com tela de arame, um canteiro que tem as medidas indicadas na figura abaixo. Se cada metro de tela custa R$ 3,00, quanto Seu Artur vai gastar?
R$ 118,20
R$ 39,40
R$ 161,00
R$ 117,20
R$ 116,20
11
D12 – Resolver problema envolvendo o cálculo de área de figuras planas. Observe, no desenho abaixo, o esquema de um estábulo que foi construído para acomodar dez cavalos. Qual é a medida da área ocupada por esse estábulo?
140
960
34
68
280
12
D13 – Resolver problema envolvendo a área total e/ou volume de um sólido (prisma, pirâmide, cilindro, cone, esfera). Amanda comprou uma forma de bolo com formato de bloco retangular , cujas medidas internas estão representadas na figura abaixo. A capacidade máxima, em cm³, dessa forma é
3 000.
1 100.
220.
500.
600.
13
D14 – Identificar a localização de números reais na reta numérica. A reta numérica abaixo está dividida em segmentos de mesma medida. O número racional está localizado entre os pontos
G e H.
F e G.
M e N.
H e J.
L e M.
14
D15 – Resolver problema que envolva variação proporcional, direta ou inversa, entre grandezas. Márcio contratou um novo pacote de canais para sua TV a cabo. Seu provedor fez uma proposta de aumentar de 100 para 175 canais, aumentando, proporcionalmente, o valor da assinatura. Márcio pagava R$ 70,00 por mês e aceitou a proposta do provedor. Quanto ele passou a pagar?
R$ 52,50
R$ 75,00
R$ 145,00
R$ 122,50
R$ 250,00
15
D16 – Resolver problema que envolva porcentagem. Das 12 000 moradias previstas em um programa habitacional, apenas 3 000 foram construídas. Qual é o valor percentual das moradias construídas nesse programa habitacional?
30%
42%
12%
18%
25%
16
D17 – Resolver problema envolvendo equação do 2º grau. Um pedreiro usou 2000 azulejos quadrados e iguais para revestir 45 m² de parede. Qual é a medida, em cm, do lado de cada azulejo?
15.
10.
18.
13.
20.
17
D18 – Reconhecer expressão algébrica que representa uma função a partir de uma tabela. Para demonstrar como se obtém a soma das medidas dos ângulos internos de um polígono convexo qualquer, um professor propôs aos alunos que utilizas sem um quadrilátero, um pentágono e um hexágono, divididos em triângulos, como mostram os desenhos abaixo. A seguir, pediu-lhes que preenchessem a tabela, como ponto de partida. Ele esperava que seus alunos concluíssem que a soma das medidas dos ângulos internos de um polígono qualquer, com n lados, é dada por:
S = 2n + 180°, pois nas figuras é possível verificar que em um polígono de n lados haverá 2n
triângulos.
S = 2.180° . n, pois nas figuras é possível verificar que há no mínimo dois triângulos nos polígonos.
S = (n – 2) · 180°, pois na tabela é possível verificar que o número de triângulos é dois a menos do que o número de lados.
S = n · 180°, pois na tabela é possível verificar que para a soma se tem a sequência de 1 em 1, até n.
S = (n + 2) · 180°, pois na tabela é possível verificar que o número de lados é dois a mais do que o número de triângulos.
18
D19 – Resolver problema envolvendo uma função do 1º grau. Um objeto está em movimento com velocidade constante. A posição desse objeto em função do tempo pode ser calculada através da expressão D = 5 + 25t, em que D representa a posição, em metros, e, t, o tempo, em segundos. Para percorrer uma certa distância, o objeto gastou 65 segundos. Qual é a posição desse objeto após percorrer essa distância?
1 620 metros.
2,4 metros.
2,8 metros.
1 950 metros.
1 630 metros.
19
D20 – Analisar crescimento/decrescimento, zeros de funções reais apresentadas em gráficos. Observe abaixo o gráfico de uma função real definida no intervalo [− 5, 7]. Essa função é estritamente decrescente
no intervalo [– 2, 0] e no intervalo [3, 5].
no intervalo [– 5, 0].
no intervalo [1, 4].
no intervalo [5, 7].
no intervalo [– 5, 2] e no intervalo [0, 3].
20
D21 – Identificar o gráfico que representa uma situação descrita em um texto. A previsão do tempo para uma cidade brasileira foi noticiada da seguinte maneira: “Durante a madrugada a temperatura diminuiu, permanecendo constante pela manhã, mas aumentou no período da tarde”. Qual dos gráficos abaixo melhor representa a situação descrita nesse texto?
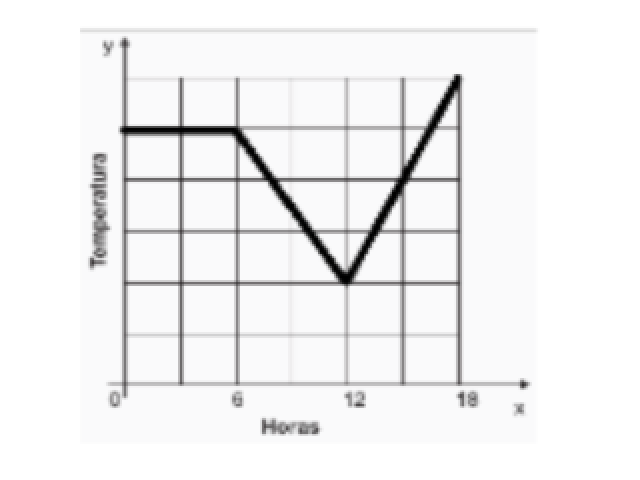
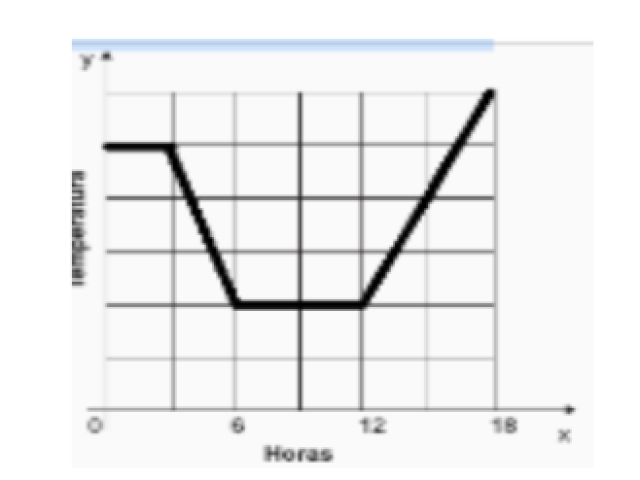
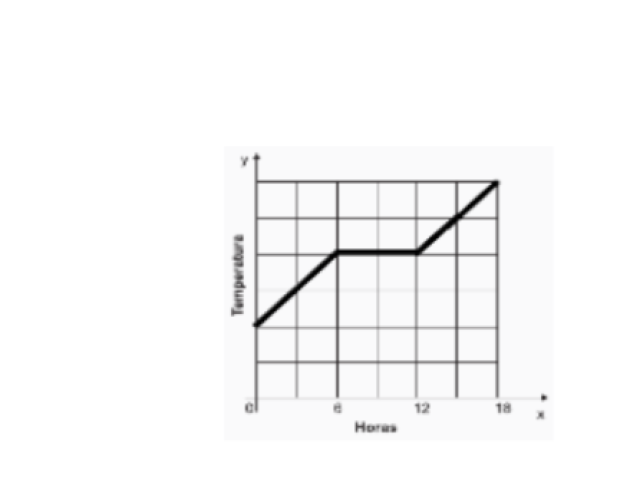
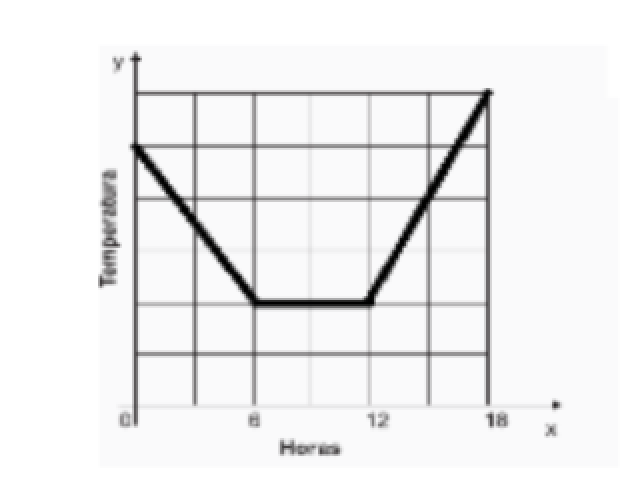
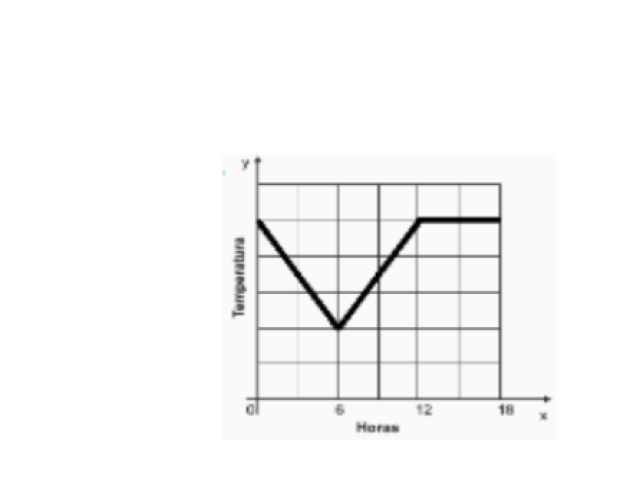
21
D22 – Resolver problema envolvendo P.A./P.G. dada a fórmula do termo geral. O diretor de uma escola resolveu melhorar sua biblioteca. Para tanto, pediu aos alunos que o ajudassem trazendo para a escola no primeiro mês 2 livros, no segundo mês 3 livros, no terceiro 4 livros e, assim, sucessivamente. Quantos livros os alunos deveriam trazer no décimo segundo mês?
11
12
14
15
13
22
D23 –Reconhecer o gráfico de uma função polinomial de 1º grau por meio de seus coeficientes. Observe a reta de equação y = mx + n desenhada no plano cartesiano abaixo.
m > 0 e n < 0.
m > 0 e n > 0.
m < 0 e n > 0.
m < 0 e n < 0.
m > 0 e n = 0.
