1
No estudo de limite, analisamos o comportamento das funções. Por exemplo, quanto maior o valor de, haverá um comportamento para os resultados da função que pode exemplo ser crescente ou decrescente, ou seja, variando os valores de vamos buscar analisar os valores de. Após a análise do problema apresentado, avalie as asserções a seguir e a relação proposta entre elas. I. Quando existe uma função definida em um intervalo aberto, contendo, exceto o próprio, dizemos que o limite de quando se aproxima de é. PORQUE II. Para todo existe um tal que sempre que A respeito dessas asserções, assinale a alternativa correta.
As duas asserções são verdadeiras, e a segunda não justifica a primeira
A primeira asserção é falsa, e a segunda é verdadeira.
As duas asserções são verdadeiras, e a segunda justifica a primeira.
As duas asserções são falsas.
A primeira asserção é verdadeira, e a segunda é falsa.
2
Em cálculo, são abordados vários tipos de funções, cada uma com um comportamento e características específicas, que refletem na representação gráfica e nas estratégias de resolução. Por isso, antes de estudar as aplicações, é importante conhecer e reconhecer cada tipo de função, como reconhecer a função: Nomeie a função apresentada acima e assinale a alternativa correspondente abaixo.
Função irracional
Função polinomial
Função inversa
Função trigonométrica
Função logaritmo
3
Em diversos contextos, podemos ter a representação matemática utilizando limites de funções, e tanto a variável independente pode tender a mais ou menos infinito quanto a variável dependente pode tender a valores infinitesimais. Para isso, é necessário analisar o comportamento da função, além de ser possível fazer uma tabela estimando valores para analisar o comportamento do limite.
+ ∞
-1
- 1/3
1
- ∞
4
A aplicação das funções trigonométricas está principalmente associada a situações em que ocorre um comportamento cíclico, uma oscilação periódica incluindo aplicações na acústica, vibrações como sinais de rádio, comunicação marítima, radares e movimento ondulatório. Considerando as informações apresentadas e o seu conhecimento sobre funções, aplique as proposições sobre funções trigonométricas e identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir. 1. ( ) cosseno 100° = seno 190° 2. ( ) seno 135° = cosseno 225° 3. ( ) seno 30° = cosseno (75°) Assinale a alternativa que apresenta a sequência CORRETA.
V - V - F
F - V - V
V - F - V
V - V - V
5
A representação gráfica das funções relaciona os valores da variável independente e da variável dependente, formando pares ordenados que são representados no plano cartesiano ortogonal, com o eixo das ordenadas e o eixo das abscissas formando um ângulo de 90°. Assinale a alternativa que corresponde à distância entre dois pontos de um gráfico.
Corresponde à hipotenusa, cujos catetos são as diferenças entre as coordenadas x e y.
Corresponde à diferença das coordenadas x ao quadrado mais o quadrado da diferença em y.
Corresponde à projeção ortogonal das diferenças das coordenadas x e y.
Corresponde à diferença dos valores x ao quadrado menos o quadrado da diferença em y.
Corresponde à raiz quadrada das coordenadas x mais as coordenadas y.
6
O uso da representação de intervalos é utilizada para identificar o domínio e a imagem de funções. Essas informações são a base para a análise do comportamento das funções. Em algumas aplicações, utilizamos as informações como raízes de uma função polinomial para chegar na função, ou, quando se trata da equação que representa uma circunferência, utilizamos as coordenadas do centro da circunferência e o valor do raio. Considerando o apresentado, avalie as afirmações a seguir e as relacione adequadamente aos temos às quais se referem. 1 - Equação da circunferência de centro em (2, -1) e raio 3. 2 - Equação da circunferência de centro em (-2, 1) e raio 3. 3 - Função polinomial com raízes 2 e -1. 4 - Função polinomial com raízes -1, 2 e 3.
1 - III; 2 - IV; 3 - I; 4 - II
1 - I; 2 - II; 3 - III; 4 - IV
1 - IV; 2 - III; 3 - II; 4 - I
1 - IV; 2 - II; 3 - I; 4 - III
1 - II; 2 - IV; 3 - I; 4 - III
7
Alguns problemas, inclusive de aplicações de cálculo na engenharia e em outras áreas, são caracterizados por limites infinitesimais, ou seja, um limite onde a variável independente tende a +∞ ou -∞ . Quando isso ocorre, precisamos analisar o comportamento da função.
- ∞
0
+ ∞
2
3
8
Quando se trata do estudo de funções, há alguns tipos de funções, cada uma com suas características específicas. Ao analisar a função, são analisados os valores de entrada e de saída e como eles se relacionam. Por isso, é importante analisar o domínio, a imagem e o comportamento da função. Nomeie Xn = ln e assinale a alternativa correspondente.
Continuidade
Imagem
Sequência
Contradomínio
Domínio
9
No cálculo, é necessário entender o comportamento das diferentes funções, assim como as funções transcendentais, onde cada tipo possui definição e características específicas. Essas características se refletem nas representações geométricas, na resolução para encontrar as raízes entre outras informações. Considerando as informações apresentadas e o seu conhecimento sobre funções transcendentais, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir:
V - V - V
V - F - V
V - V - F
V - F - F
F - V - V
10
ㅤㅤㅤㅤㅤㅤ
Reta concorrente
Reta tangente
Taxa de variação
Curva de tendência
Taxa de anulação
11
Em muitos casos, ao olhar a função na qual deseja calcular o limite, se substituir o valor a que x está tendendo, cairá em uma indeterminação. Por isso, faz-se necessário aplicar técnicas que proporcionem resolver o limite sem cair na indeterminação. São essas técnicas que são importantes para a resolução de problemas de limite.
3
0
-1
2
1
12
ㅤㅤㅤㅤㅤㅤ
V - V - F
V - F - F
F - V - F
F - V - V
V - F - V
13
ㅤㅤㅤㅤㅤㅤ
- 1/4
4
1/4
-4
0
14
ㅤㅤㅤㅤㅤㅤ
1 - II; 2 - IV; 3 - III; 4 - I
1 - III; 2 - IV; 3 - I; 4 - II
1 - II; 2 - III; 3 - IV; 4 - I
1 - II; 2 - IV; 3 - I; 4 - III
1 - IV; 2 - II; 3 - III; 4 - I
15
ㅤㅤㅤㅤㅤㅤ
interior, direita, contínua, esquerda
interior, esquerda, contínua, direita
interior, direita, descontínua, esquerda
exterior, esquerda, descontínua, direita
exterior, esquerda, contínua, direita
16
Um dos desafios em calcular a derivada de funções é analisar se a função é derivável em todos os pontos de seu domínio, só em alguns pontos ou, ainda, se em alguns pontos não é derivável. Essa análise está associada à definição de derivada, bem como à função contínua. Após a análise do problema apresentado, avalie as asserções a seguir e a relação proposta entre elas.
As duas asserções são verdadeiras, e a segunda não justifica a primeira.
As duas asserções são verdadeiras, e a segunda justifica a primeira.
A primeira asserção é verdadeira, e a segunda é falsa.
A primeira asserção é falsa, e a segunda é verdadeira.
As duas asserções são falsas.
17
A derivada do quociente de duas funções não é o quociente de suas derivadas. Também temos a regra da soma e da potência que pode ser aplicada para obter a derivada de uma função.
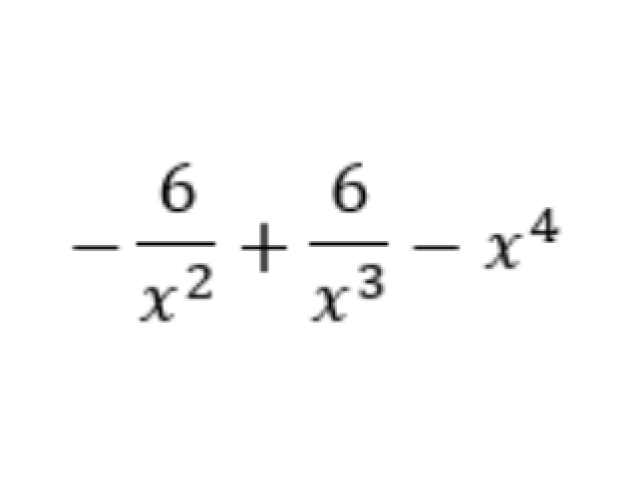
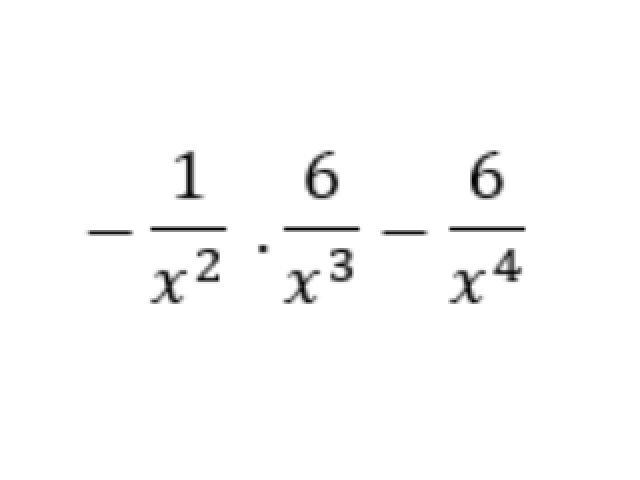
18
Podemos calcular a derivada de diversas funções. No estudo das derivadas, iniciamos calculando a derivada de funções simples, cada uma com sua característica, para, depois, aprofundar o estudo com problemas que envolvem mais de uma característica, como calcular a derivada da função y = sen x * cos x Resolva o problema acima e assinale abaixo a alternativa que corresponde à resposta.
cos² x - sen² x
- cos² x + sen² x
1
cos x - sen x
- cos x * sen x
19
Alguns problemas de cálculo de derivada necessitam que, antes de realizar a derivação propriamente dita, a função seja reescrita para uma função equivalente (que se aproxime das funções cuja derivada é conhecida). Esse procedimento é necessário para facilitar a aplicação de técnicas e de regras de derivação de funções.
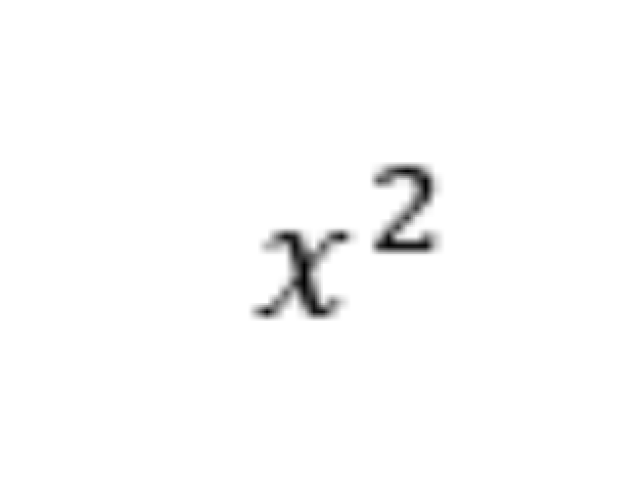
20
ㅤㅤㅤㅤㅤㅤ
Função quociente
Função modular
Função composta
Função exponencial
Função produto
21
Há algumas regras sobre o cálculo de derivada, como a regra da potência. É importante reconhecer qual regra utilizar para calcular a derivada. Para isso, é importante reconhecer as características da função de que deseja calcular a derivada e, assim, aplicar a regra mais apropriada. Observe as informações sobre as regras abaixo.
1 - IV; 2 - III; 3 - II; 4 - I
1 - II; 2 - III; 3 - IV; 4 - I
1 - III; 2 - IV; 3 - I; 4 - II
1 - II; 2 - IV; 3 - I; 4 - III
1 - IV; 2 - II; 3 - III; 4 - I
22
ㅤㅤㅤㅤㅤㅤ
A primeira asserção é verdadeira, e a segunda é falsa.
A primeira asserção é falsa, e a segunda é verdadeira.
As duas asserções são verdadeiras, e a segunda não justifica a primeira.
As duas asserções são falsas.
As duas asserções são verdadeiras, e a segunda justifica a primeira.
23
ㅤㅤㅤㅤㅤㅤ
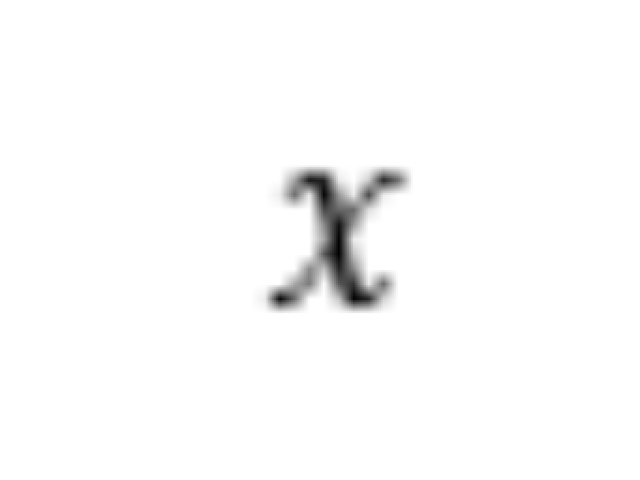
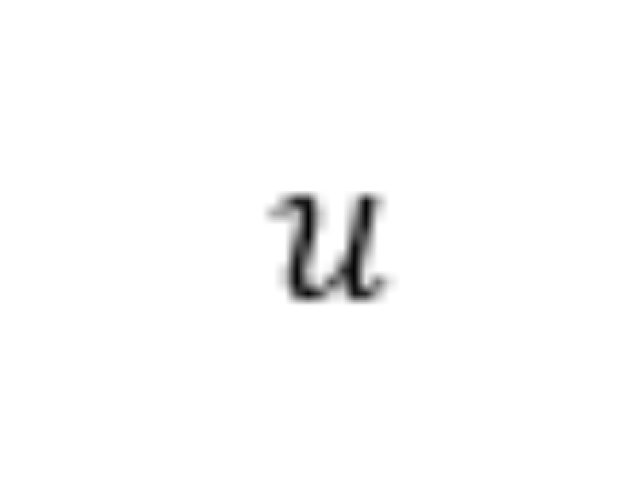
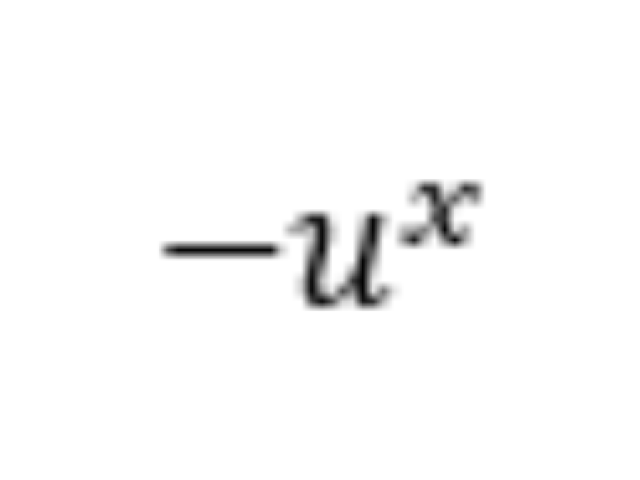
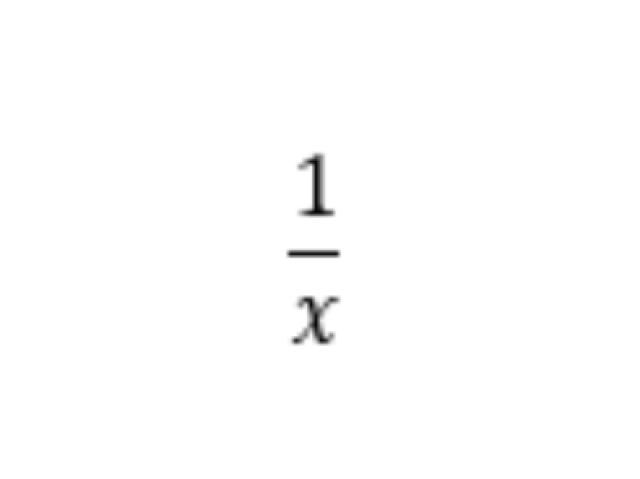
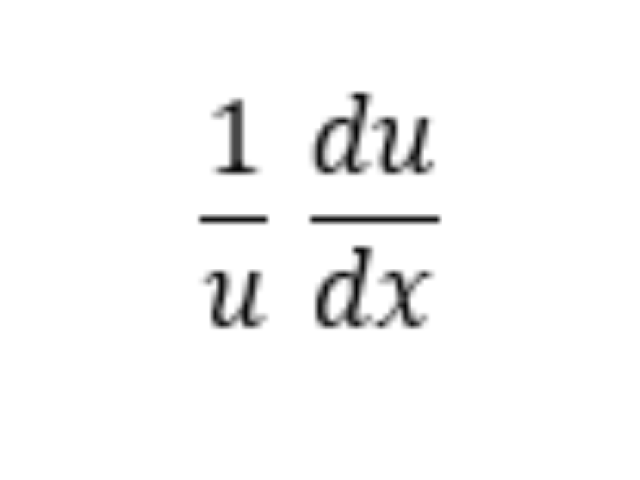
24
ㅤㅤㅤㅤㅤㅤ
diferenciável, nunca, não tem, qualquer
diferenciável, nunca, tem, todo
diferenciável, nunca, não tem, todo
descontínua, sempre, tem, qualquer
contínua, sempre, não tem, todo
25
ㅤㅤㅤㅤㅤㅤ
As regras de L'Hospital garantem que, se as duas funções forem contínuas, então existem derivadas, e, significa que há um valor de tendência representado pelos limites
As regras de L'Hospital garantem que, se as duas funções forem descontínuas, então existem derivadas, e significa que não há um valor de tendência que possa ser representado pelos limites
As duas regras de L'Hospital garantem que, se pelo menos uma das duas funções for contínua, então existem derivadas, e significa que há um valor de tendência representado pelos limites
As regras de L'Hospital garantem que, se as duas funções forem contínuas, então não existem derivadas e nem há um valor de tendência que possa ser representado sem o uso de derivadas
As regras de L'Hospital garantem que, se pelo menos um das duas funções for contínua, então existem derivadas, e significa que há um valor do tendência representado pelos limites
26
Os polinômios, também, estão presentes no cálculo de uma variável independente; por isso, analisamos as características e aplicamos técnicas de resolução para obter derivadas. A partir da análise da função, é possível compreender o comportamento dela, como ao analisar: y = x³ + 3x² - 2x - 1 para o domínio de -{3,1}. Considerando as informações apresentadas e o seu conhecimento sobre pontos de máximos e mínimos, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir. I. ( ) A derivada segunda de um ponto extremo de uma função indica se o ponto é máximo ou mínimo. II. ( ) Para investigar os pontos de máximo e mínimo, é necessário encontrar os valores de x onde existe y"=0. III. ( ) Para essa função, temos y"=6x+6. Assinale a alternativa que apresenta a sequência CORRETA.
V - F - V
V - V - F
V - F - F
V - V - V
F - V - V
27
Seja a função f(x) - x³ - 2x² + x - 1, temos que, para analisar o comportamento desta, é necessário calcular os pontos críticos igualando a derivada à primeira a zero e resolvendo-o, para obter as raízes que levam a zero. Assim, para essa função, temos dois pontos críticos. Resolva as derivadas à primeira e à segunda da função acima e assinale a alternativa que corresponde ao ponto x = 1.
Máximo local
Ponto de decrescimento
Mínimo local
Ponto de crescimento
Ponto de interseção
28
É verdade que as regras de L'Hospital são aplicadas em casos de cálculo de limite, em que temos resultados como ou . Nesses casos, aplicamos as regras de L'Hospital, relacionando com o cálculo de derivada e obtendo resultados diferentes de: ou . Defina os casos descritos acima e assinale a alternativa correspondente.
Indeterminação.
Diferenciável.
Continuidade.
Inflexão.
Descontinuidade.
29
Muitos comportamentos são descritos por funções, como o crescimento de plantas em uma fazenda, a propagação de doenças em uma localidade geográfica ou o crescimento de árvores em uma área de reflorestamento. Contudo é necessário verificar se, em determinado ponto da função, ela é crescente ou decrescente. Assinale a alternativa que apresenta, corretamente, o cálculo realizado para verificar crescimento ou decrescimento de uma função.
Derivada.
Continuidade.
Integral.
Imagem.
Domínio.
30
ㅤㅤㅤㅤㅤㅤ
II e III, apenas
I e IV, apenas
I e III, apenas
I e II, apenas
III e IV, apenas
31
ㅤㅤㅤㅤㅤㅤ
1 - I; 2 - II; 3 - III
1 - III; 2 - II; 3 - I
1 - II; 2 - III; 3 - I
1 - II; 2 - I; 3 - III
1 - III; 2 - I; 3 - II
32
ㅤㅤㅤㅤㅤㅤ
mínimo, existir, máximo, fechado
mínimo, não existir, máximo, aberto
máximo, não existir, mínimo, fechado
mínimo, existir, máximo, aberto
máximo, existir, mínimo, aberto
33
ㅤㅤㅤㅤㅤㅤ
4
0,04
0,3
1,3
0,03
34
Quando temos o gráfico de uma função, a área abaixo dessa curva pode ser calculada como a soma da área de vários retângulos que tentam preencher a área abaixo da curva. Quanto menor a área da base dos retângulos, mais próximo do valor real da área, ou seja, para isso, é necessário dividir o intervalo em várias partes. Como se chama o procedimento que calcula a área abaixo da curva de função em um dado intervalo? Assinale a alternativa correspondente.
Integral de Riemann.
Teorema de Taylor.
Regra de L'Hospital.
Regra da cadeia.
Pontos de inferência.
35
ㅤㅤㅤㅤㅤㅤ
Integral de Riemann
Teorema fundamental do cálculo
Descontínua
Primitiva
Derivada
36
Um teorema é uma afirmação matemática que já foi provada por meio de deduções e provas e a partir de axiomas. Por isso, você pode utilizar o teorema fundamental do cálculo para resolver problemas em que exista uma integral definida em um dado intervalo [a,b], sem precisar provar sua veracidade. Após análise do problema apresentado, avalie as asserções a seguir e a relação proposta entre elas. I. O teorema fundamental do cálculo fornece informações para obter um valor numérico, ou seja, um número como resultado. PORQUE II. Descreve como usar o intervalo da integral definida e a primitiva da função para obter esse resultado numérico. Analisando as asserções anteriores, conclui-se que:
as duas asserções são verdadeiras, e a segunda justifica a primeira.
a primeira asserção é verdadeira, e a segunda é falsa.
a primeira asserção é falsa, e a segunda é verdadeira.
as duas asserções são verdadeiras, e a segunda não justifica a primeira.
as duas asserções são falsas.
37
O teorema fundamental do cálculo fornece orientação de como resolver uma integral definida, pois considera o intervalo [a,b] (em que a integral está definida) na resolução do problema. Aplique o teorema fundamental do cálculo para f(x) = 3x² + 2 no intervalo de x=1 até x=2. Aplique o cálculo de área em f(x) e assinale a alternativa correspondente.
10
4
8
12
9
38
ㅤㅤㅤㅤㅤㅤ
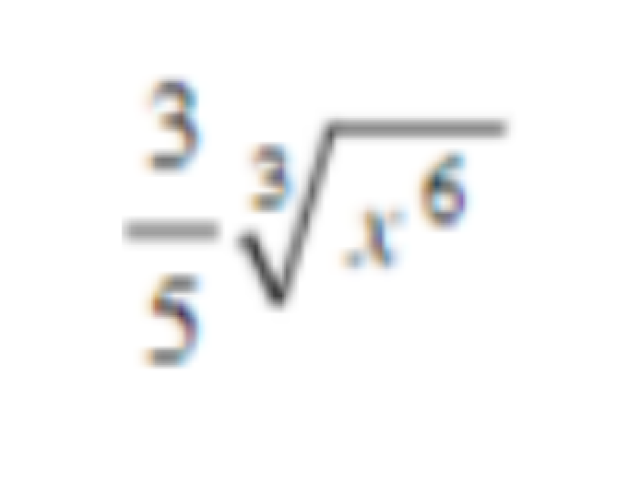
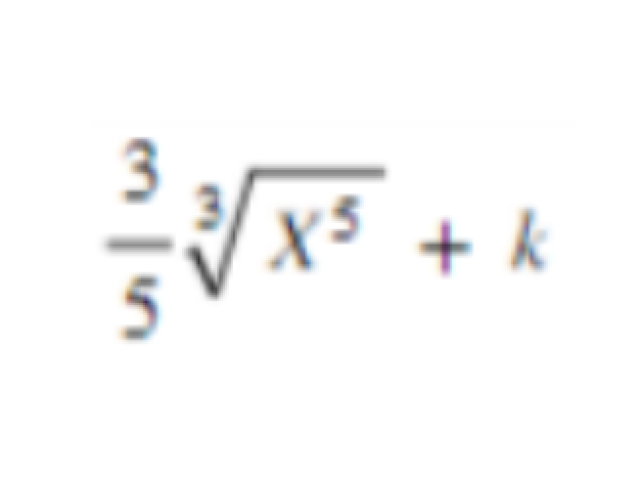
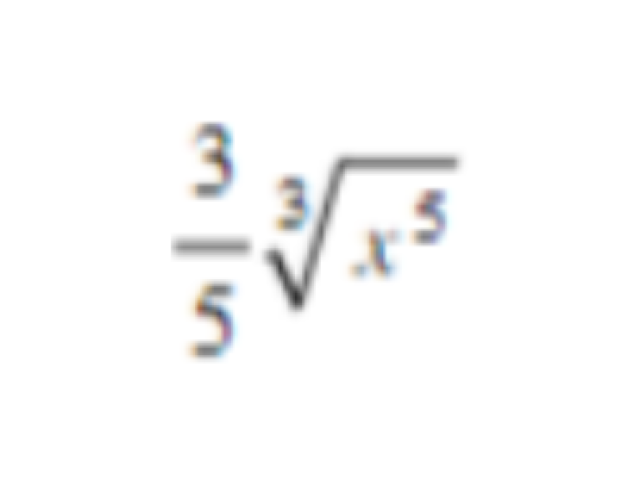
39
![O estudo sobre integral de Riemann fornece informações para resolver vários problemas relacionados ao cálculo da integral. Considerando
as funções f(x) e g(x) integráveis no intervalo [a,b], temos algumas propriedades da integral em decorrência da definição de integral de Riemann.](/_image?href=https%3A%2F%2Fimg.quizur.com%2Ff%2Fimg6428f6a4c24257.47097854.png%3FlastEdited%3D1680406185&w=400&h=400&f=webp)
O estudo sobre integral de Riemann fornece informações para resolver vários problemas relacionados ao cálculo da integral. Considerando as funções f(x) e g(x) integráveis no intervalo [a,b], temos algumas propriedades da integral em decorrência da definição de integral de Riemann.
4
12
1
8
2
40
As integrais indefinidas não têm um intervalo de integração, mas servem para encontrar a função original a partir de sua derivada. Seja f uma função definida no intervalo I, temos que, para todo x, teremos uma função F definida em I, de forma que F'(x)=f(x) . Nomeie F e assinale a alternativa correspondente.
Descontínua
Integral de Riemann
Primitiva
Derivada
Teorema fundamental do cálculo
41
![O estudo sobre integral de Riemann fornece informações para resolver vários problemas relacionados ao cálculo da integral. Considerando as funções f(x) e g(x) integráveis no intervalo, [a,b] temos algumas propriedades da integral em decorrência da definição de integral de Riemann. Considerando f(x)=8x³ e g(x)=4+3x², analise as informações a seguir.](/_image?href=https%3A%2F%2Fimg.quizur.com%2Ff%2Fimg6428f6f73c38c9.13302171.png%3FlastEdited%3D1680406265&w=400&h=400&f=webp)
O estudo sobre integral de Riemann fornece informações para resolver vários problemas relacionados ao cálculo da integral. Considerando as funções f(x) e g(x) integráveis no intervalo, [a,b] temos algumas propriedades da integral em decorrência da definição de integral de Riemann. Considerando f(x)=8x³ e g(x)=4+3x², analise as informações a seguir.
1 - II; 2 - III; 3 - I
1 - II; 2 - I; 3 - III
1 - III; 2 - II; 3 - I
1 - I; 2 - II; 3 - III
1 - I; 2 - III; 3 - II
42
Há diversas funções e, consequentemente, diversas técnicas de primitivação. Por isso, existem tabelas para consulta, contudo é fundamental dominar as técnicas de primitivação das principais funções, inclusive para entender o funcionamento das técnicas e aprimorar as habilidades relacionadas à resolução de problemas. Considerando as informações apresentadas e o seu conhecimento sobre as técnicas de primitivação, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir.
V - V - F
F - V - F
V - F - V
F - V - V
V - V - V
43
As primitivas imediatas são aquelas que são obtidas de funções simples, ou seja, não há a presença de funções compostas. Lembrando que funções compostas são aquelas em que uma função está no lugar da variável independente de outra função. Por isso, a representação de uma função dentro da outra. Considerando as informações apresentadas e o seu conhecimento sobre as técnicas de primitivação, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir.
V - F - V
V - V - V
F - V - V
V - F - F
V - V - F
44
Em alguns casos, temos que calcular a integral de funções compostas, como y=sen (x²), onde temos a mistura da função f(x) = sen x e g(x) = x², que ao descrever a função f°g=f(g(x)) = sen (x²). Há outros casos onde temos uma função dentro da outra, a questão é como calcular a primitiva para esse tipo de função. Após análise do problema apresentado, avalie as asserções a seguir e a relação proposta entre elas.
as duas asserções são verdadeiras, e a segunda justifica a primeira.
as duas asserções são falsas.
a primeira asserção é falsa, e a segunda é verdadeira.
as duas asserções são verdadeiras, e a segunda não justifica a primeira.
a primeira asserção é verdadeira, e a segunda justifica a primeira.
45
Há algumas regras sobre o cálculo de integral, como integração por partes. É importante reconhecer qual regra utilizar para calcular a primitiva. Para isso, é importante reconhecer as características da função para a qual deseja calcular a primitiva e, assim, aplicar a regra mais apropriada. Observe os grupos de informações sobre regras que seguem abaixo:
1 - II; 2 - III; 3 - I
1 - III; 2 - I; 3 - II
1 - I; 2 - II; 3 - III
1 - II; 2 - I; 3 - III
1 - III; 2 - II; 3 - I
46
ㅤㅤㅤㅤㅤㅤ
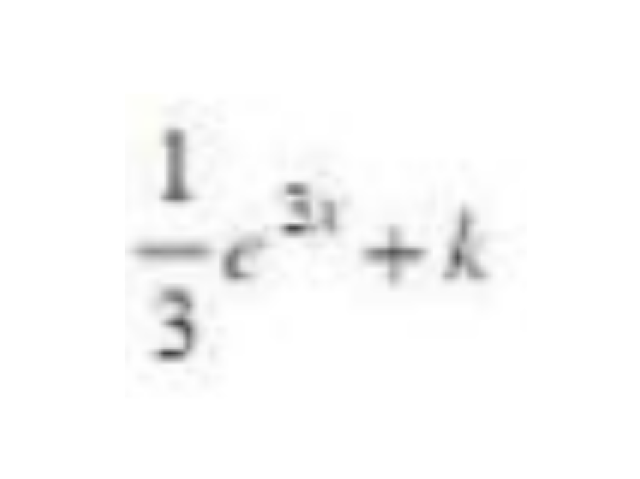
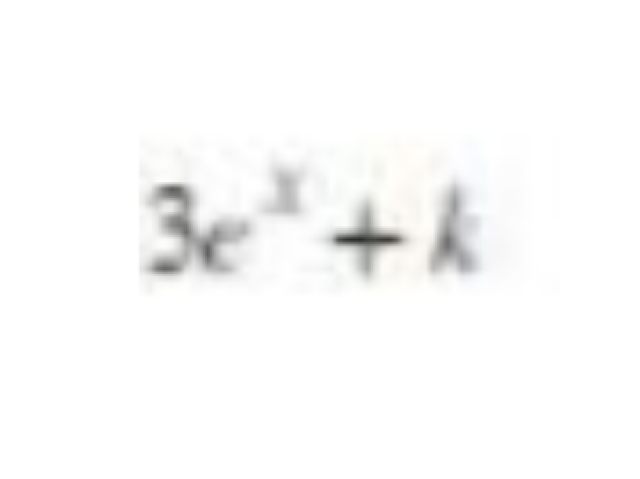
47
ㅤㅤㅤㅤㅤㅤ
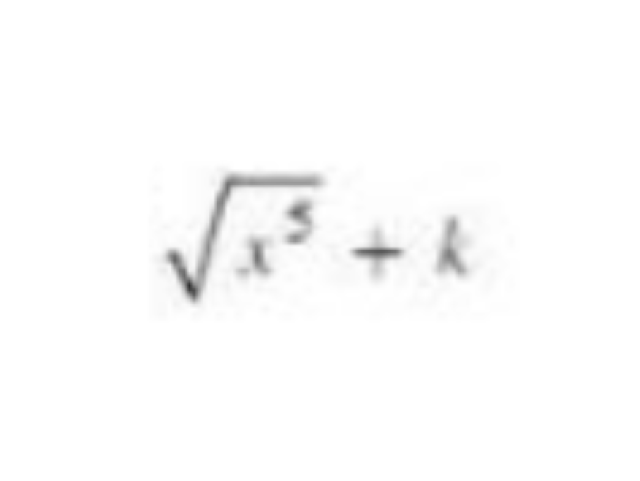
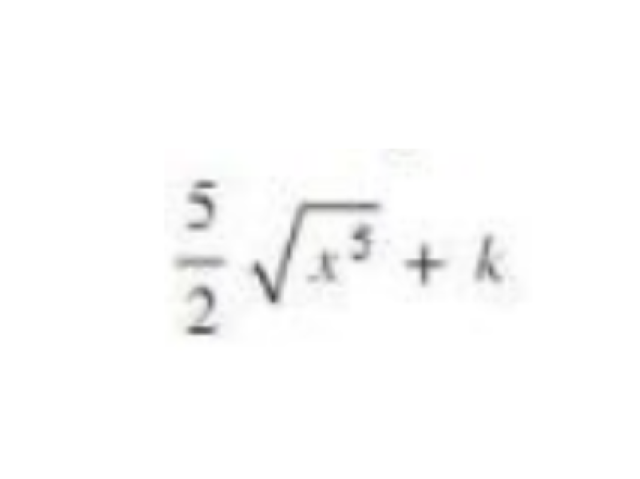
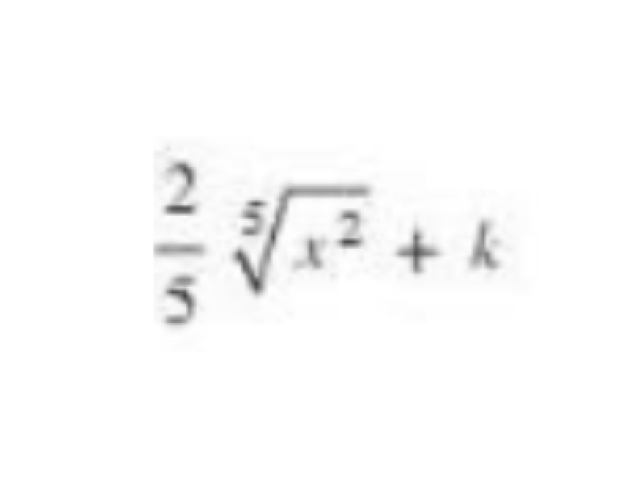
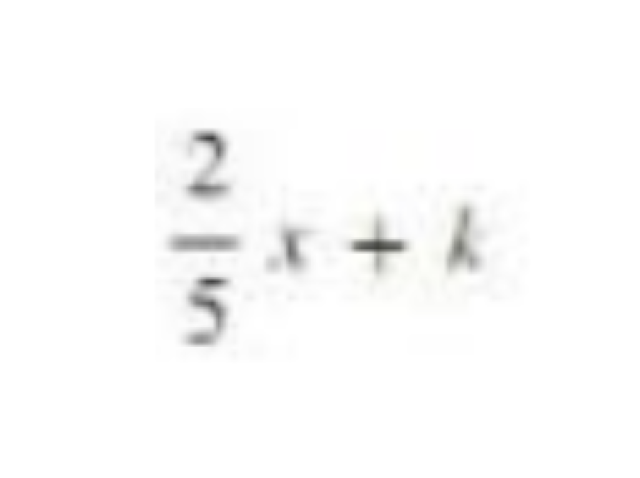
48
ㅤㅤㅤㅤㅤㅤ
definida, derivável, não seja, é
indefinida, derivável, seja, é
definida, não derivável, seja, não é
indefinida, não derivável, seja, não é
indefinida, derivável, não seja, é
49
ㅤㅤㅤㅤㅤㅤ
x² = 2u
x² = u
x + 1 = sen u
x + 1 = cos u
x + 1 = tg u
50
Aplicamos os conceitos relacionados às primitivas imediatas para resolver as integrais de funções compostas. Lembrando que funções compostas são aquelas em que uma função está dentro da outra. Por isso, é fundamental dominar as técnicas de primitivação e aprofundar os estudos realizando muitos exercícios. Considerando as informações apresentadas e o seu conhecimento sobre as técnicas de primitivação, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir.
V - F - V
F - V - F
F - V - V
V - F - F
V - V - V
51
O cálculo da área limitada por um gráfico de uma função definida em um intervalo [a,b] é uma aplicação do cálculo diferencial integral e tem alguns passos em uma ordem específica. Esses passos são como uma receita de bolo, na qual é necessário respeitar a ordem. Considerando as informações apresentadas e o seu conhecimento sobre cálculo de área limitada por uma função, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir. I. ( ) O cálculo da área abaixo da curva é uma aplicação direta da regra de L'Hopital que enuncia a soma das áreas de pequenos retângulos abaixo da curva do gráfico de uma função. II. ( ) Quando se trata da interseção de dois gráficos é necessário analisar as funções e o intervalo para então verificar qual área deve ser subtraída e então escrever algebricamente. III. ( ) Não existe área negativa, independente do tipo da função mas ao calcular a integral de algumas funções chegamos em um valor negativo que indica que a área está abaixo do eixo x. Assinale a alternativa que apresenta a sequência CORRETA.
F - V - V
V - F - F
F - F - V
V - F - V
V - V - F
52
Alguns problemas são limitados por dois gráficos, além das retas paralelas ao eixo y que interceptam o eixo x nos pontos que correspondem ao intervalo, no qual se deseja calcular a área, como a área limitada por x=0, x=1, y=2 e y=x². Resolva o problema de calcular a área limitada pelos valores descritos acima e assinale a alternativa que corresponde à área.
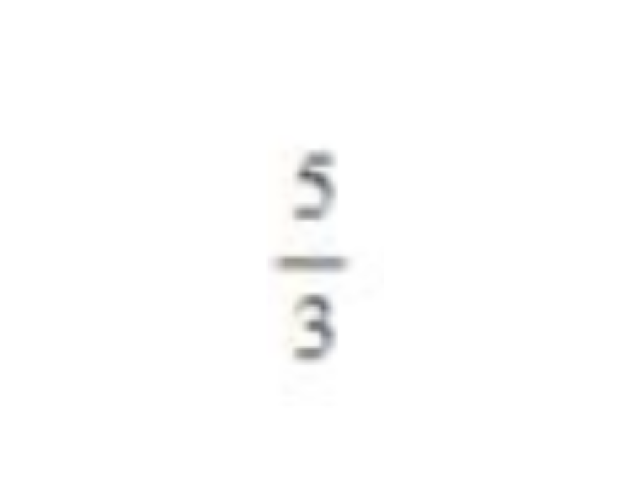
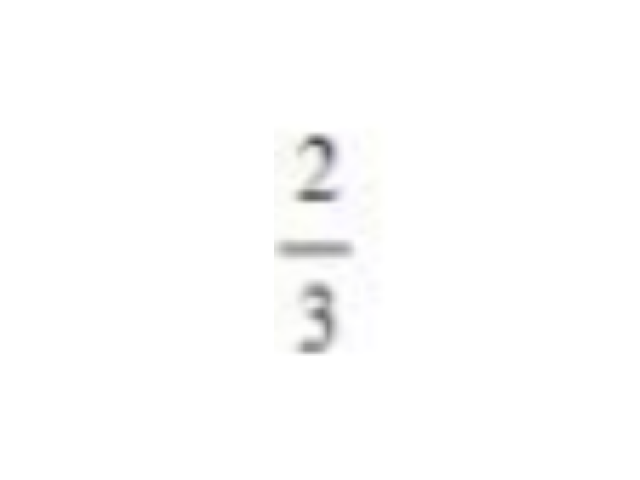
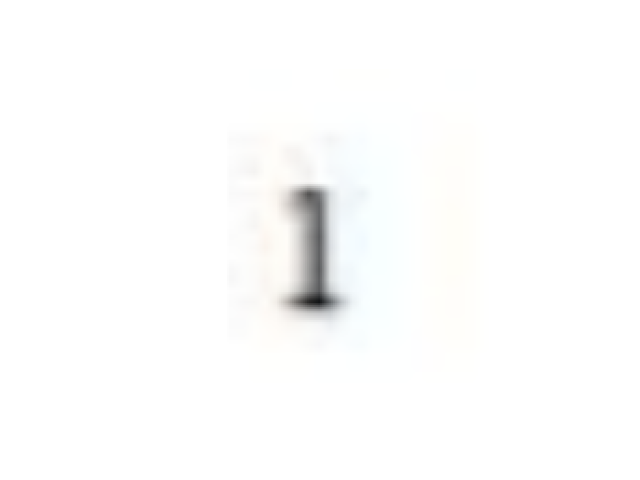
53
Quando calculamos a área limitada pelo gráfico de uma função, consideramos a área limitada pelo eixo cartesiano x e o gráfico da função. Contudo, para a função f(x)=x³ no intervalo x=-1 até x=1, ao aplicar a integral, o resultado é zero, mas ao rascunhar o gráfico é visível que existem duas áreas e que a soma dessas áreas não será negativa. Esse é um problema que exige outra estratégia de resolução para cálculo da área. Após análise do problema apresentado, avalie as asserções a seguir e a relação proposta entre elas. I. Para calcular a área limitada pela função x³, é necessário separar em dois intervalos. PORQUE II. Assim, será possível somar as áreas sem que se anulem.
as duas asserções são falsas
a primeira asserção é falsa, e a segunda é verdadeira
a primeira asserção é verdadeira, e a segunda é falsa
as duas asserções são verdadeiras, e a segunda justifica a primeira
as duas asserções são verdadeiras, e a segunda não justifica a primeira
54
Alguns problemas de integração, incluindo os problemas de aplicação onde é calculada a área limitada pela função, podem apresentar funções conhecidas como integrais impróprias. Como exemplo, temos uma partícula que se desloca sobre o eixo , com a velocidade representada pela função: v(t)=3-t . com t em minutos. Com relação às informações acima, analise as afirmações a seguir.
I e III, apenas
I e IV, apenas
I e II, apenas
III e IV, apenas
II e III, apenas
55
Considere uma função f(x)=4 e a área formada abaixo dessa função, ou seja, entre o gráfico dessa função e o eixo cartesiano ortogonal x. E, considerando a área limitada pelas retas x=-1 e x=3, observe que as retas x=-1 e x=3 são paralelas ao eixo cartesiano ortogonal y. Diga qual é a área do problema descrito acima e assinale a alternativa correspondente.
12
10
8
16
4
56
Calcular a área limitada por um gráfico, dada uma função e um intervalo [a,b], é uma aplicação do cálculo das integrais, em especial, uma aplicação da integral definida. Essa aplicação está, diretamente, associada a um teorema, pois resulta da definição desse teorema. Diga o nome do teorema que resulta no cálculo de área limitada por uma função e assinale a alternativa correspondente.
Teorema de L'Hospital.
Teorema de Taylor.
Teorema do sanduíche.
Teorema fundamental do cálculo.
Teorema da integral indefinida.
57
ㅤㅤㅤㅤㅤㅤ
2
1/2
∞
4
1
58
Há diversas funções e, consequentemente, diversas técnicas de primitivação. Mas, para todas as funções, incluindo as funções compostas, é possível calcular a área limitada por um gráfico e definida em um intervalo [a,b]. Por sinal, essa técnica é a aplicação de um teorema. Considerando as informações apresentadas e o seu conhecimento sobre cálculo de área limitada por uma função, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir. I. ( ) O resultado do cálculo da área é um número. II. ( ) É uma aplicação da integral indefinida. III. ( ) Utiliza o intervalo [a, b] na resolução. Assinale a alternativa que apresenta a sequência CORRETA.
F - F - V
V - V - F
V - F - F
V - F - V
F - V - V
59
Quando calculamos a área __________ pelo gráfico de uma função, consideramos a área limitada pelo eixo cartesiano __________, o gráfico da função e duas retas paralelas ao eixo __________. As retas paralelas ao eixo __________ são definidas pelos pontos que interceptam o eixo x, definindo, assim o intervalo. Preencha as lacunas escolhendo a alternativa CORRETA.
limitada, x, y, x.
descontínua, y, x, x.
limitada, x, y, y.
limitada, x, x, y.
descontínua, y, y, x.
60
Há diversas funções e, consequentemente, diversas técnicas de primitivação. Mas, para todas as funções, incluindo as funções compostas, é possível calcular a área limitada por um gráfico e definida em um intervalo [a,b]. Por sinal, essa técnica é a aplicação de um teorema. Considerando as informações apresentadas e o seu conhecimento sobre cálculo de área limitada por uma função, identifique se são (V) verdadeiras ou (F) falsas as afirmativas a seguir. I. ( ) O resultado do cálculo da área é um número. II. ( ) É uma aplicação da integral indefinida. III. ( ) Utiliza o intervalo [a,b] na resolução. Assinale a alternativa que apresenta a sequência CORRETA.
V - F - F
V - V - F
V - F - V
F - F - V
F - V - V
